※指導内容の例
【中1数学】
A町から22km離れたB町に自転車で行くのに、はじめは時速9kmで走り、途中のP町から時速15kmで走ったら、A町からB町まで2時間で行くことができた。時速9kmで走った時間は何時間か。
右のような図を描いてみる。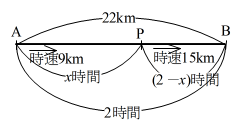
時速9kmで走った時間を\(x\)時間とすると、A町からP町まで\(x\)時間で走ったということになる。
時速15kmで走ったのはP町からB町で、ここにかかる時間は\((2-x)\)時間と表せる。
ここで道のりを考えてみる。
道のり=速さ×時間の公式を使おう。
A町からP町の道のりは\(9 \times x=9x\)kmとなり、
P町からB町までの道のりは\(15 \times (2-x)=15(2-x)\)kmとなる。
A町からB町までの道のりが22kmであるので、
\(9x+15(2-x)=22\)という方程式ができる。
\(9x+30-15x=22\)
\(9x-15x=22-30\)
\(-6x=-8\)
\(\displaystyle x=\frac{4}{3}\)
となり、これは問題に合っている。
よって、時速9kmで走ったのは \(\displaystyle \frac{4}{3}\) 時間となる。
普通にやるとこのような説明になりますが、当塾では他の分野にも応用が利く別の解き方を教えることができます。
詳しくは、体験授業で!
【中3数学】
関数\(y=2x^2\)のグラフ上に2点A,Bがあり、\(x\)座標はそれぞれ-1,3である。
このとき、直線ABの式を求めよ。
右のような図を描いてみる。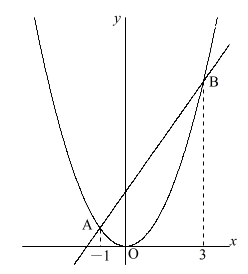
点Aの\(x\)座標が-1なので\(y=2x^2\)に代入して\(y=2 \times (-1)^2=2\)となる。
同様に、点Bの\(x\)座標が3なので、\(y=2 \times 3^2=18\)となる。
よって、A(-1,2),B(3,18)とわかる。
この2点の座標からABの傾きを求めると、
\(\displaystyle \frac{18-2}{3-(-1)}=\frac{16}{4}=4\)
直線の式を\(y=4x+b\)とおく。
点Aの座標を代入して
\(2=4 \times (-1)+b\)
よって、\(b=6\)
したがって直線ABの式は \(y=4x+6\) となる。
普通にやるとこのような説明になりますが、当塾ではもっとシンプルな別の解き方を教えることができます。
詳しくは、体験授業で!
【大学入試】
「円周率が3.05より大きいことを証明せよ」(2003東京大学)
この問題を解くカギとなる説明は、小学生のときに習っています。
たぶん東大もそれを踏まえた上で出題したと思われます。
高校生は当然、三角比(\(\sin\)とか\(\cos\)とか)を使って解くわけですが…。
実は、中3までの知識があれば証明できます。
詳しくは、体験授業で!
※無料体験の申込 0836-34-4900
携帯・スマホからは080-5610-6684
